刚刚我们说完了,关于圆的相关知识,接下来我将首先从正方形开始,向你们说明一些基本平面几何图形的定义性质等知识。
那么首先从正方形开始吧。
那么首先让我们看一张图片。(我终于弄到一个效果好点的图了)

显然,这是一个窗户。
如果你只关注这六个构成大的窗户的小方形的话,你会感觉还有一种整齐的美感。
好吧,我不太会描述,总之,你会发现无论是横着来量,还是竖着来量的话,它的长度是差不多的。
那么,如果它的长度真的是相同的会怎样呢?
在这个例子中,如果长度真的相同,那么我们就可以说,它是一个正方形。当然仅限于此例。
当然,为了让我说的话更加的准确,我们将类似于圆那样对这个所谓的正方形进行人为的定义。
但同时像上一章那样用画出一个该图形的步骤来对它进行定义有点繁琐。
我不妨直接给你一个正方形。

如果你能靠这一张图就学会如何画正方形的话,那可真是太好了。
接下来我将向你介绍组成正方形的部分。
显然,正方形可以认为是由四条线段组成的,但我想像你说的是这四条线段的特点。
首先便是这四条线段必须具有相同的长度,否则,他将不是一个正方形。
其次,仔细的观察一下这四条线段两两交汇的地方。
你会发现他们看起来都一样。
但是在数学里用这样的语言来描述可不是什么好事。
想一想我们应该用什么来准确地描述这种关系?
当然是角度了。
我又重新看了看之前,发现自己2千字竟然都在扯角度是什么。
不过没关系,你现在一定非常清楚角度是什么了。
总之,不要扯那些别的了,我只想告诉你正方形两两线段之间的角都有一个特殊的名字,叫做直角。
这名字很恰当吧?你感觉这两条线段是不是都有一种很直的感觉?严谨的来说是这两条线段的关系很直。
事实上,为了帮助你理解什么是直角,也许我们要先说些别的。
我们都知道重力是竖直向下的,而我们认为地平线是直的。
因此,一个静止的物体在只受重力的情况下运动的轨迹与地面所成的夹角就是一个直角。
当然,直角的定义可能不是这样的,但我想这应该是最而易见的理解怎样才算“直”。
接下来我将告诉你,怎样对一个角才算是直角。
随意的取两条直线,如图:
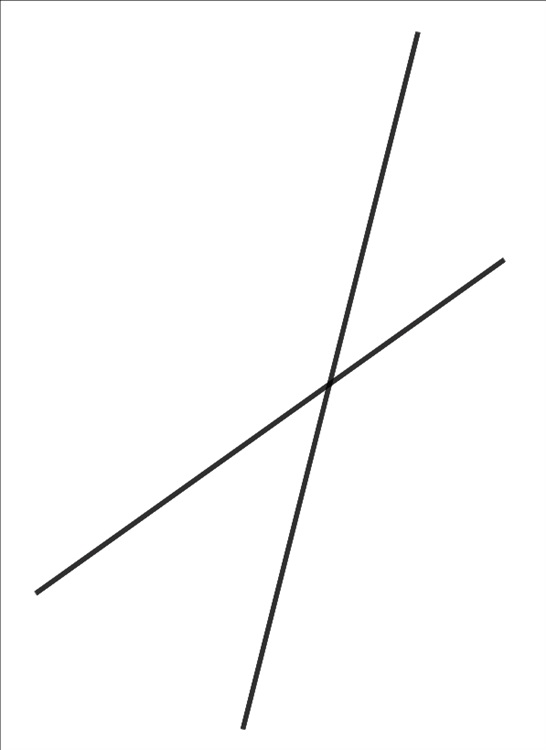
你应当能看出这两条直线形成了四个角。
你可以试着随意的旋转这两条直线中的其中一个,直到出现如下情形:

当这四个角的角度都一样时,我们就可以认为这四个角都是直角。当然,此时的两条直线,有一种特殊的位置关系,这被称为垂直。
一般的,我们认为,如果你能证明两条直线的夹角中有一个为直角,那么我们就认为这两条直线垂直。
反之亦成立。也就是说,如果有两条垂直的直线,那么这两条直线所构成的夹角为直角,并且四个角都为直角。
好了,这应当能帮助你很好的解决判断它是不是直角的问题。
不过,接下来我仍将为你展示真正的定义。
《几何原本》中的定义:当一条直线和另一条横的直线交成的邻角彼此相等时,这些角的每一个被叫做直角。
以上一段为几何原本中的定义。
还没有我们说的好呢,对吧?
接下来我们要做的就是用角度来度量直角了。
一般的,我们把旋转一周认为是360度。
例如,如果在一个圆中,随意的做一条半径,如图:
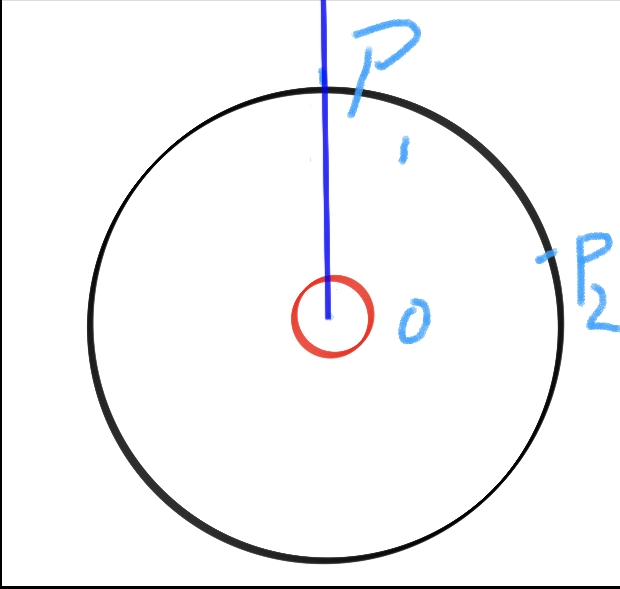
为了方便我们就仍然取这张图了,你只需要注意蓝色的半径就可以。
如果该半径保持圆心不动,而另一点在圆上一动的话,我们就可以说该半径在旋转。
同理,任何线段,只要以其中的一个端点为固定点,另一点在保持该线段长度不变的情况下移动,这种行为被称为旋转。
但是,旋转并不一定意味着要以线段的其中一个端点为固定点。
你可以以该线段上的任意一点为固定点。
事实上,旋转的本质就是以某一点为圆心画一个圆,但是没有轨迹,也就是说没有圆弧,只剩下最后停止移动时的终点,此时该终点与原固定点之间的连线就可以被认为是原线段进行了旋转。例如端点的情况。
如果以任意一点为固定点的话,相对来讲,更难理解。
事实上,你可以认为,此时是以线段的固定点分别到线段的两端点所形成的两段线段为两个半径画两个圆,并最终形成两条新的线段。此时,若你只看其中一条线段的话,他与我们之前所讲的端点的情况其实是完全相似的。
也就是说,以固定线段上任意一点旋转可以认为是将该线段一分为二进行两次旋转。
所以其本质上仍然可以认为是旋转。
那么,现在我们终于把旋转给说完了。
说的好长,所以我再把这幅图直接放在下面,免得你回去在翻页:
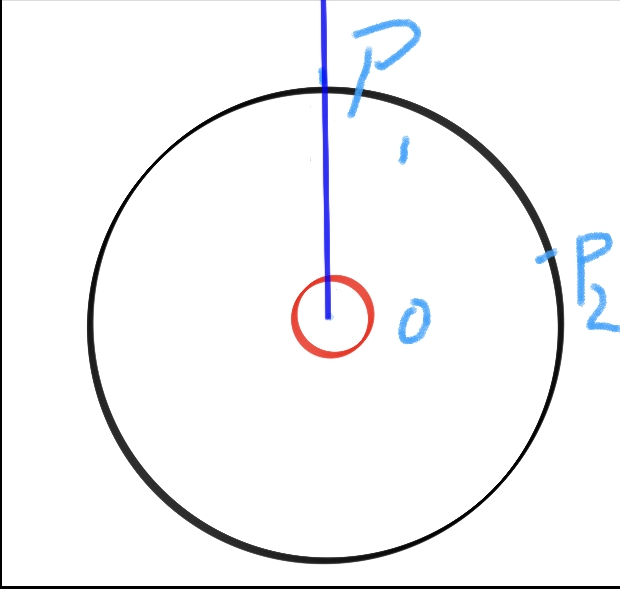
如果把这条蓝色的半径以圆心为固定点旋转的话,当他固定一个方向,比如说向左,或者是向右,当然,你需要注意到当他旋转到这个圆的另一边时他的向左向右会和直观上的向左向右有点区别。
比如说当它向左旋转到这个圆的下面时,对于该半径来说,如果他要继续向左旋转,实际上是我们人眼直观上的向右旋转。
我相信这个问题比较简单。如果越说会越糊涂,所以我们就到此为止。
那么当他旋转到初始位置时,我们就称呼它为旋转一周。
一般的,我们用角度来衡量旋转一周,我们认为旋转这一周需要转过360度。
那么直角是其1/4,显然直角的度数应该为90度。当然,如果反过来的话也是成立的。也就是说,如果有一个角为90度,那么它就是直角。
很好,我们现在终于说明白了什么是直角。
我们终于能对正方形下一个定义了。当然有一个非常显而易见的事情,不要忘记了,那就是正方形是由四条线段所组成的。并且更显而易见的是,这四条线段都是连着的。
让我们开始吧:
如果有一由四条线段所构成的平面图形,这四条线段的长度都相等,且首尾相连,并且在两两相连处所形成的角度均为90度,也就是直角,那么我们就可以认为该平面图形是一个正方形。
只是一个定义就花了一整章啊。
那么我们接下来,将继续深入研究正方形及其他基本的平面几何图形。














