我们刚刚说到只要证明了在两个三角形中,如果有任意两个角相等,就能够证明这两个三角形的三个角两两分别对应相等。
现在让我们加上一个条件,除了有两个角对应相等之外,还有一组边也是对应相等的。
当然,一开始我们还是找一些特殊的情况吧,比如,就像我们之前所提到的那样,这一组对应相等的边恰好在这两个角中间。
如果画图直观的来说明的话,大概是下面这样。
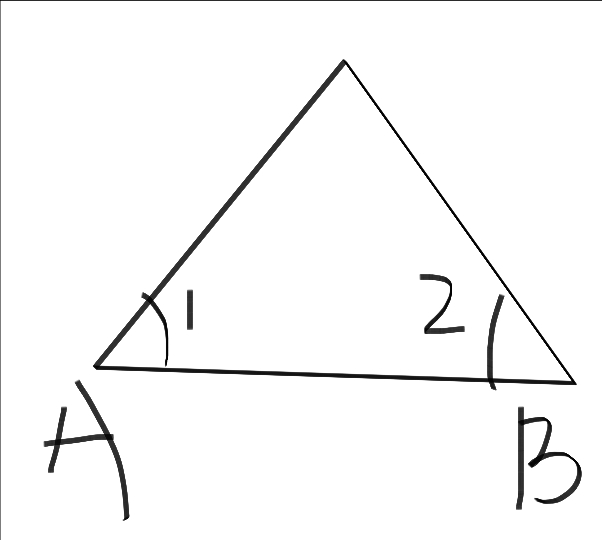
如果角一和角二是对应相等的角的话,那么AB就是对应相等的边。顺带一提,你能够根据我们以前学过的东西来严谨的定义一下,什么叫做两角夹着的边吗?如果是我的话,我可能会把这条边称为,角一和角二的公共边。即使是第一次听到公共边这个概念,你也应该明白他的意思。公共边就是只两个角共用一个边。直观的来说,就是直线AB既是角一的一个边,又是角二的一个边。
好了,我们接下来将开始处理我们的真正困难,那就是加上一组边对应相等后,如何证明这两个三角形全等?
我们仍然将从最基本的点线关系入手,来帮助我们解决这个问题。再次整理一下我们的已知条件以及要证明的结果。
在两个三角形中,有两组角对应相等,并且在这两个三角形中,这两组对应角所分别夹着的那一边也对应相等。而我们要证明的是,这两个三角形全等,也就相当于是所有的边和所有的角都对应相等。
好了,把这些都列出来就显得一目了然了,接下来只需要证明就可以了。
不过,如果直接证明的话,还是有点困难,所以我们不妨换一种角度思考一下。
我给你这样一个问题:如果已经确定了一条线段,并以这条线段的两个端点分别作为角的顶点,并且以该线段所在的直线为角的一边,以两个固定的角度来分别画出相应的另外两条直线。
问题来了!这两条直线的交点是否是确定?
当然是确定了的!你可以这样想:这条确定的边有两个确定的端点,加上确定的角度就有两条确定的直线,两条被确定了的直线,当然会有一个被确定了的交点。
非常符合常理,对吧?
当然,在这里我发现我不得不再告诉你一些东西。
当然很简单,这些都是基本事实。
1.两点确定一条直线。
你有办法有三个点出画一条直线吗?一般情况下三个点,你不能画出一条直线,并使这条直线经过这三个点。而若是你真的成功了,那么随意的去掉一个点吧,然后你会发现用另外两个点画出的直线仍然是该直线。
2.两点也能确定一条线段。
如果给了两个确定了点,让不同的人以该两点作为一条线段的两个端点的话,会有人画出与他人不同的情况吗?显然不会。
3.一个点和一个角度能确定一条直线。
如果给你一个确定了的点,让你以一定的角度来画一条直线,会有几种情况呢?显然也只能有一种吧?顺带一提,角度有时候也相当于有另一个确定的点。
4.两条确定的直线有一个确定的交点。
这也很好理解。除非这条直线是弯的,否则交点一定是确定的。当然,这里确定的意思是完全相同,包括其中一条直线不能用它的一条平行直线来替换,否则交点的位置就会改变。当然,对于直线这种向左右两边无限延长的东西来说,不管交点往哪边移动,又移动了多少,对于以前的位置来说,相对于这两条直线本身几乎可以认为是不变的。毕竟移动的这一点位置相对于直线本身无限的距离来说,可以看成是零了。
对于这种想法,我们在以后的学习中还会用到。事实上,我建议你尽可能的记住,并尝试着去使用包括这种方法在内的各种独特的方法,也许下一个要载入史册的数学家就会是你呢?
不过对于上述所说的第4点,其实我还有一点要说:两条不平行的直线,一定相交于一点。
几乎相当于是废话,对吧?显然不平行,一定会相交啊。不过,严谨一些总没有问题,对吧?至少在数学里。
到这里,我把我现在能想到的一些可能要用到的基本事实都告诉你了,这样当我们以后再遇到相似问题时,我们就不用像现在证明勾股定理一样,去提前证明这么多东西了。
话说你有没有发现?我们为了证明勾股定理已经学了很多东西了。感觉到数学的严密了吗?差一步,我们都可能会无法完成某个看似很简单的证明。
我们本应该继续去证明沟股定理的,毕竟有关于三角形全等的一种方法,我已经说了,这足以使我们证明勾股定理。至少在我们所使用的这种图中足够了。
不过我刚刚还向你说了一些基本事实,那么我们现在不妨趁热打铁,让我再告诉你五个基本事实。
1、等于同量的量彼此相等。
2、等量加等量,其和相等。
3、等量减等量,其差相等。
4、彼此能重合的物体是全等的。
5、整体大于部分。
这是欧几里德在《几何原本》中所提到的五个基本事实。这五条不需要你去证明,它是如何成立的,因为真的没有比他更基本的东西了。
事实上,我们之前所提到的所有东西基本上可以认为是由这五条来证明的。
我们只是把这五条的内容运用在了一些我们想象中的抽象东西上。
比如点,线,其实本质上是我们对现实生活中某些东西的抽象,而我们人为定义了一些东西,并发现这样定义有一些好处,而这些定义能够给我们带来的东西,都是按照这五个基本事实来确定的。
比如我们之前说的三角形内角和等于180度时,其实就运用到了,其中的第三条,也可以认为是第二条,倒个位置而已,没什么本质区别。
别问我为什么不把二三简化成一个,因为我也想问。
总之,我想告诉你的是,数学被建立在一个逻辑之上,如果这个逻辑最根本的地基都是坏的,那么我们在这个地基上所建造的一切都是毫无意义的。
幸好,直到现在,我们还没有搞出这么大的麻烦。
好了,到这一章,我们终于把证明勾股定理前所有需要准备的东西都说完了。
下一章,我们终于可以继续证明勾股定理了。














