突然想起,我还是没有说到用勾股定理证明正方形的性质啊。
不过没关系,多项式间的乘法比较简单,因为我们在上一张基本已经证明了,我只需要再向你解释一下,我们为什么说已经证明了就ok了。
我们今天一定会说到正方形的性质的。
先说多项式之间的乘法运算法则。
不过为了解决这个问题,我想我要先向你说明一下乘法运算所具有的法则。
为了方便,我将用小写字母,比如a和b用来表示某些具体的数,此时这个小写字母就可以被称为虚拟变量。如果在课本中的话,这个内容应该被称之为用字母表示数。
事实上,关于这种思想,我们早已在之前的方程就见到过了。你只需要知道的是,他能代表任何数。记住,是任何数。这一点我们将在后面多项式间的乘法法则提到,他将会是我们解决问题的关键。
我现在很想向你转示乘法间的基本关系,但在哪之前先让我们整理一下,所有的运算吧!
首先是加法,我们在前面已经提到过了,两个数相加,几本质上就是用一个数,把这两个数表示出来,相当于把这两个部分合成一个整体。你应当对其运算的意义和方法十分熟悉。
而我要提到的就是有关用符号表达时的一些运算顺序问题。
比如a+b+c,显然,我可以表示成b+a+c,或者a+c+b。事实上,你想怎么换就怎么换,主要还是这三个数,它们之间用加号连接就可以。
无论你把加法的这几个数如何变换位置,都不会对最后的计算造成影响。加法的这种性质被称为加法交换律。
就像字面意思那样,你可以交换,但结果不变。
在这里我要引入一个概念,括号。(好吧,又一次用没说过的东西来解释了)括号代表着你需要先算括号内部的任何运算。记住,是任何!
括号被表示为这个:()
当然,一般情况下括号不会单独出现,他里面一定是有计算的。一般而言,其外部也有计算,否则为什么要专门加一个括号的?但有特殊情况,比如我们之前说到的,关于计算结果单位的问题。
你来看看这个:a+(b+c)。这与a+b+c的结果是否一样呢?根据括号的定义,我们应该先算括号内的运算。也就是说先算b+c,然后再用这个结果加a。那么当然是一样的了,这个不就相当于是计算b+
c+a嘛?而根据我们刚刚学过的加法交换律,他显然等于a+b+c。所以,他的本质与加法交换率一样,这是因为先加哪个后加哪个对结果是毫无影响的。
就算你计算你的年工资一样,你从1月到12月按顺序加可以,你倒过来加也可以,或者你随意,想怎么加就怎么加都可以,只要别发某一个加了两次就行。
所以,括号其实就是交换的另一种形式,或者说基本质是一样的。
但由于这个括号确实让他看上去不太一样,所以我们称呼他为加法结合律。
没想到我们在加法就说了这么多,接下来还是加快进度吧!
首先,乘法也具有这两种性质,这分别被称为乘法交换律和乘法结合律。因此,这相同的两点,我们就不再说了。
我们要说说乘法不太一样的,另一个性质。
请看下面这个式子ax(b+c)等于什么?这我们昨天所提到的相似,根据乘法的定义,以及括号内要先算的法则,这个式子表达的含义就是a个“b+c”相加,那么你当然可以理解成a个b加上a个c,也就是a×b+a×c。
这一点应当是很好理解的。
值得注意的是,由于我采用了虚拟变量,他可以表示任何数,也就是说,我们证明了所有的数都可以把上面那种形式转化为下面这种形式。
也就是说对任意三个数,有:ax(b+c)=a×b+a×c。
乘法的这种性质被称为乘法分配律。
就像他的名字一样,这种括号外相乘的关系被分配到了括号内每个被加的数上。
好了,到这里我们就说完了,接下来继续说说多项式间的乘法吧!
事实上,我在上一章解释勾股定理时所推理的过程就可以被看作是证明多项时间相乘的过程,如果你在这一方面不会的话,那么我建议你应该再回顾一下这一部分内容。
或者,你可以使用两次乘法分配律,这样就能让你比较清晰地认识到多项式之间乘法的本质。
那么关于乘法之间的内容,大概就到这里了,接下来就让我们继续说回正方形的性质吧!
首先,让我们先来画一个正方形。
如图:
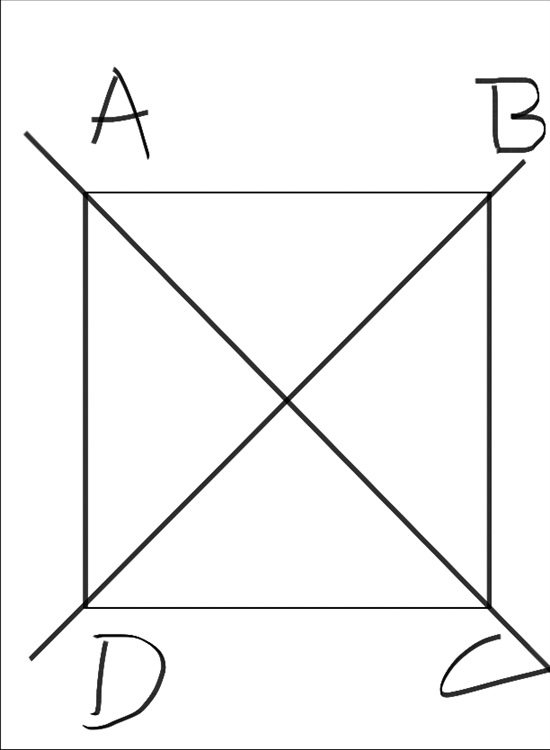
这是一个正方形ABCD,我们很容易的知道三角形ADC和三角形BCD都是直角三角形,并且AD等于DC等于BC。
根据我们之前学过的勾股定理,AC的平方就等于AD的平方加上DC的平方,BD的平方就等于BC的平方,加上DC的平方。根据我们前面知道的,这三个直角边都是相等的,所以很容易的,就能证出来任意两个的平方和相加也是相等的。也就是说:AC的平方等于BD的平方。
所以AC等于BD。
当然,我们以后会认识到,两个数的平方相等,并不意味着这两个数相等,这是因为有负数的存在。
但在这个例子中,作为一个直角三角形的斜边,他的长度不可能为负数。所以这两个数都为正,且相等。
所以,我们就证明了正方形的对角线相等。这就是正方形的其中一个性质。
不过现在来看,也许运用三角形全等的知识来证明更加好。
没关系,至少我们学会了勾股定理。这真的是一个很重要的知识点,我们以后在很多地方都会用到它。
接下来,我们将继续学习有关三角形全等的知识。
事实上,也许先学三角形这个三边形,对于我们解决包括正方形在内的众多四边形是一个更好的选择。
所以,我们在下一章将继续研究三角形全等的条件。














