在上一章,我们已经说完了,所有的通用的三角形证全等的方法。无论是怎样的三角形,只要满足上一章中所说的四种全等方法的任意一个,那么我们就可以成功的证明出两个三角形全等了。
但在三角形中有一个很特殊的三角形,那就是直角三角形。他非常的特殊,特殊到我们要专门研究只有在直角三角形中才能证明全等的方法。
简单来说,我们需要更多的方法来证明直角三角形全等,因为它太重要了。我们甚至不去研究除此之外的其他类型的三角形了。
那么接下来我们就回到正题吧!
首先,已经提到过的四种证明全等的方法,仍然是适用于直角三角形的。因为那是对于所有的三角形都适用的方法,而直角三角形作为三角形中的一类,当然也能使用这四种方法来证明全等了。
接下来我们将试着探寻新的方法。
一听到直角三角形,你也许会想着从角度的方向去研究,因为他先天就带着一个直角,所以相当于是天然给我们增加了一个条件。
不过,正如我们之前提到过的一样,只靠角度是无法判断两个三角形全等的。哪怕两个三角形的三个角完全对应相等,这也并不代表着这两个三角形就全等。
所以,无论是哪种方法,你必须要确保有一个边是对应相等的。这一点在我们之前已经证明过的四种方法中都可以体现,因为在这四种方法中,每一个条件中都有至少一组边对应相等。
也就是说,无论怎样,你都至少要加上一个与边相关的条件。
那么加上直角三角形自带的直角条件,你就有了一边一角两个条件。
而我们之前也提到过,证明全等是要以最少的条件去证明的。而我们知道三个条件是最少能证明全等的条件,所以即使是在直角三角形中,你也要尽力的去保证只用三个条件就能证明出直角三角形全等。
如果你在这一边一角两个条件的基础上加任意一个角,这实质上就相当于是以前的AAS或ASA,因为你知道两个角后根据内角和定理你就知道了三个角,无论你加上哪个边,都与这两种方法一模一样。
所以我们试着换一条路走,我们加上一个边。
这样就相当于是有两边和一个角。同时,为了防止与SAS相重合,我们还要确保这两个边不能同时是这个直角三角形的两条直角边。
而三角形只有三个边,所以只能是一个斜边和一个直角边相等了。
让我们试试它能不能证明出两个直角三角形全等吧!当然,我们还是选择把它简化为:已知直角三角形的任意一个直角边和斜边,能否画出唯一的一个直角三角形。
如图:
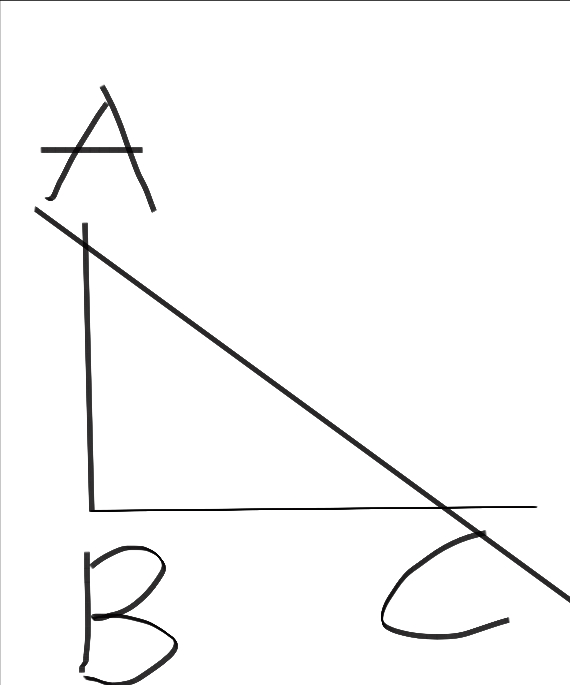
如果AC和AB确定了,这个三角形是确定的吗?
让我再帮你稍微转换一下思想,过点A,以AC做为半径画圆,这个圆的交点,与这个直角的另一边,也就是BC,能否只形成一个交点?
如果只有一个交点的话,那么肯定就只有一个确定的三角形了。
不要被我所画出的这幅图所迷惑,如果你能在脑海中把这幅图补全的话,也就是把直线BC往左延长,然后把这个圆画出来,你就会发现在左边还有一个交点。
毕竟只要有直角就行了嘛,可没有对直角冲着哪边有要求,对吧?
但是虽然有两个交点,但我们仍然可以说形成的三角形是确定的。
简单来说,你只是把他反了个个而已,跟我们之前的一样,就像照了个镜子。
只是颠倒一下左右的话,当然不会有什么影响了。就像你转个身,难道你就不是你了吗?
如果你认为这还不足以解释的话,那么我只能说你确实是一个严谨的人,我们在以后学习的另外一些知识后,将会更好的来解决这个问题。
所以,我们认为既然只能画出一个确定的三角形的话,那么如果两个直角三角形都有一个直角边和一个斜边相等的话,我们就认为这两个直角三角形全等。
这种方法被称为HL。就像ASA,SSS,这种全等方法的命名一样,H和L分别表示直角三角形的斜边和直角边。
当然,使用这种证明全等的方法最重要的一个前提就是,一定要在直角三角形里使用它。
到目前为止,我们算是说完了,这种直角三角形里特殊的证明全等的方法。
除了在刚才的证明那里好像稍微不太好,对吧?
那么我们就换一种方法吧,我们将使用我们最近学到的新知识来很好的解决这个问题。
还是刚刚的条件,在两个直角三角形内,已知这两个三角形的斜边对应相等,一组直角边对应相等。
那么根据我们学过的勾股定理,另一直角边的平书就等于斜边的平方减去已知直角边的平方。由于斜边的平方和已知直角边的平方都分别相等,所以另一直角边的平方也一定相等。
如果这另一直角边的平方相等的话,那么这另一直角边肯定也是相等的。
因为直角边不可能是负数嘛。不过我们好像并未学过平方与开方的关系,这一点我们将在以后提到。
现在,我们算是解决这个问题了吧?
因为你看,现在我们得到了什么?我们知道另一个直角边也相等了。
现在要你证明这两个直角三角形全等应该是轻而易举了吧?
你有两种方法可以用,一是根据直角相等,且夹该角的两直角边也相等,所以你可以用SAS来证明这两个直角三角形全等。我前面说过,上一章提到的这四种方法,是对于包括直角三角形在内的所有三角形都通用的证明全等的方法。
当然,你现在也知道了两个直角三角形的三个边全都相等,所以你用SSS来证明这两个直角三角形全等也可以。
总之,在直角三角形中,只要你知道一个斜边和一个直角边对应相等的话,你就能够得到这两个直角三角形全等了。
有一点我想提示一下,由于这种方法运用勾股定理,所以不要认为只要知道直角三角形的两直角边就可以使用HL。除非你用勾股定理证明斜边相等。但是有点麻烦,不是吗?事实上,如果知道在两个直角三角形中两直角边对应相等的话,那不就是一个标准的SAS证明全等的方法吗?这与HL的条件确实不一样。
除非你再多去证一下斜边也相等,否则我建议你还是直接用SAS吧。














