我们之前说完了,在直角三角形中证明全等的方法,这被简称为HL,但愿你还记得这两个字母分别代表哪两个边。
不过你应当清楚的是,其本质是运用勾股定理得出令一边关系相等,所以实质上仍然运用的是那四种基本的证明全等的方法,只不过算是一种变化而已。
而今天,我将继续带你探索各种各样不同的三角形所拥有的各种性质。
首先我要为你介绍的是有两条边是相等的三角形。
一般这种三角形,我们就可以称呼它为等腰三角形。
只要有任意两个边相等,他就是等腰三角形。此时那两个相等的边都被称为这个等腰三角形的一个腰,而一般来说,我们就可以把另外一条边称作为底边。
实际上这个符号就是个很显然的等腰三角形:△。只不过他好像底边也和两个腰相等。但这并不重要。只要有任意两边相等,那么它一定就是等腰三角形。不过对于这种三个边都相等的,一般的我们称呼她为等边三角形。非常简单吧?
接下来我将为你引入几个比较简单的定义。
中线,高线,角平分线。
最后一个很简单,你在一个角中间做一条射线,然后把这个角平均的分成两个等大的小角,此时这条射线就叫做原来那个大角的角平分线。
高线,其实是一种相对的概念。比方说如果要测量你的身高是多少,使用软尺的话,一般情况下,你应该将这个尺子拉直,并且保证他与你的身体平行且垂直于地面,当然你的身子也肯定要垂直于地面了,也就是笔直地站着。此时你的身高就被对应到了,这条卷纸上有刻度的线段,通过观察这个卷尺上面的刻度,你就可以轻松的判断出自己的身高。
此时这个身高就可以被看作是从你的身体的最高点距地面做一条高线的长度。
当然仅仅是长度了,因为高线还是要保证这条线过最高点的。
除非你把这卷尺给吞了,否则我可不认为这条卷尺能经过你的最高点。
那么让我们找个例子吧!
比方说在这个三角形中:
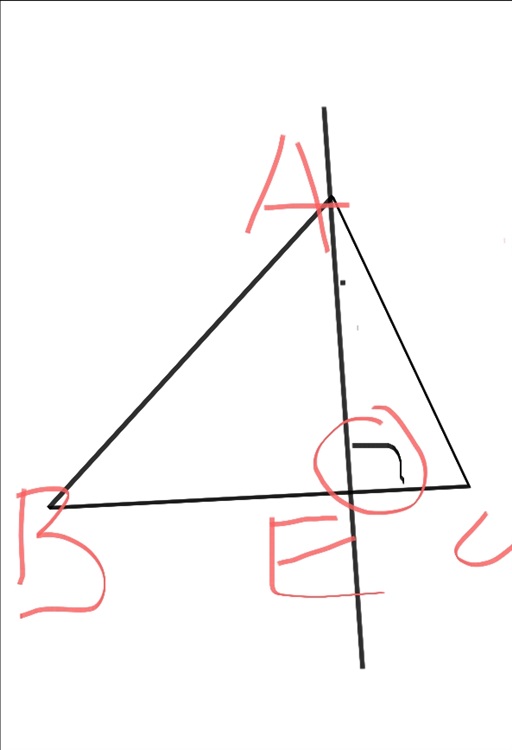
我用红色的笔写出了名顶点,以便于你能够轻松地将它和黑色的图分开。你应当注意到我在图中圈了一个红圈,红圈里有一个黑色的,一个像直角的东西。这被称为垂直符号。一般情况下,如果在两条线段之间的角度用这种标示来画出来的话,那么就代表着这两个直线垂直。
好了,给你解释完了,根据我们刚才的经验,你应该很容易的就能看出AE是这个三角形的一个高。
因为他过那个最高点A嘛,然后还恰好和底边的BC垂直。
现在你应该发现了,在三角形中三角形的高是一个相对的高,他实际上就可以被看成是三角形的一个顶点到由另外两个顶点所连成的线段的长度。
就这么简单。
值得一提的是,你应该能看出一个三角形,至少有三个高吧?
这都是很简单的东西,我们继续说中线。
实际上中线更简单。
知道中间的点吧?一般情况下中间的点就指的是某两个点之间的点。这不是废话吗?但我觉得大多数人的经验,如果要选择这么一个点的话,可能会选正中间的那个点吧?不知道你咋说,反正我喜欢选正中间的,只要他很简单就能取到的话。
因此,一般情况下中点就指的是那个,能把线段平均一分为二的那个点,就是正中间那个点。
而中线呢,就是有另外的那一个点连接该中点,所做的线就被称为中线。
很简单吧?而在三角形中,一般以这条中线上的中点所在的原来的两另外的顶点用来形容这条中线。
比如在这个例子中:
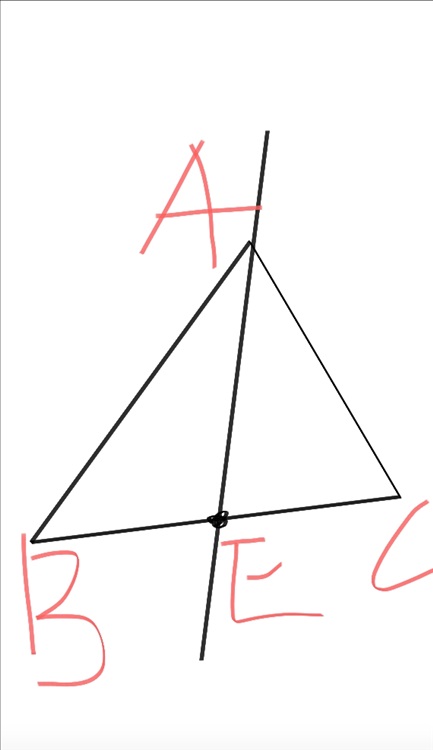
AE就是一条中线,而一般情况下我们在做出这样一条中线时,这么说,也许能够让你清楚的知道自己在做哪条中线:在三角形ABC中作BC边上的中线。
一般情况下,这样就可以了,基本不会有人理解错吧?
接下来我要说重点的了,前面只是一些概念性的东西。
在等腰三角形中,这三条线有什么特点呢?很简单,它们重合。
当然,我可不是说过任意一个顶点作这三条线都重合。这个顶点必须是那两条相等的边的交点。也就是说,这个顶点必须是等腰三角形两腰的交点。
那么接下来就让我们证明吧!
实际上证明他比较简单,我觉得我简单说说就可以了。
画图,你们应该不需要吧?
你现在可以随便的想象一个等腰三角形,但是我建议你把它摆正。这个摆正就是让你把那条与另外两边不相等的边放在底下。
就是让他左右看起来对称。
这样说吧,你把这个等腰三角形看成一个人,那两个相等的边都说了是腰了,把它看成是人的腰的两边,你要让这个人立起来!让他站起来!不要让他躺在地上。
当然,你愿意躺就躺吧, 我只是通过这个例子,让你把三角形立起来。人们躺着,可是能够思考,而三角形躺着不利于人们的思考,所以为了人类,勉为其难让三角形站一会儿吧!
好了,现在你可以继续想象这个三角形了。
你过顶点随意的做一条中线。
此时是不是把它分割成左右两个三角形?
你看一下这两个三角形有什么特点。
首先,由于他们都已新作的这条中线作为一个边,所以他们天然的有一个边对应相等啊!
其次,都说是等腰三角形了,那他两个腰肯定得相等啊!也就是说在新形成的两个小三角形中,加上前面说过的那个,已经有两组边对应相等了。
你再看看剩下的一个底边。你做的不是一条中线吗?那他肯定是平均分成两半的呀!那么这两个小三角形这三组对边不就完全对应相等了吗?
这不就是SSS证明全等的方法吗?
所以左右这两个小三角形全等,那么它上面的两个顶角肯定得一样啊!所以中线肯定还是角分线咯。再看下面。
两个角把一个平角平分,那这两个角肯定都是直角咯。所以这条线还是高线。
所以,我们成功地证明了,在等腰三角形中三线全部重合。这被称为三线合一。
当然了,如果你做另外两条线,比如你做一个高线或者是角平分线,也能够证明出三线合一。不过这算拓展了,你可以自己去试着证明一下。
总而言之,你只需要记住三线合一,这就足够了。














