为了让你更好的理解斜率这个概念,我们不得不从直线的角度来解释。
你可以这样想。由于我们刚才提到过的函数的图像是一个直线(我们先假设假设它是直线,这是为了更好地理解斜率),所以我们当然可以运用我们所了解到的有关直线的知识来理解他们。
说来惭愧,我回顾我曾经写的内容时,发现确实很混乱。如有机会,我会考虑更改的。
我接下来用到的知识在第一卷第18章提到:一个点和一个角度能确定一条直线。
一个点很好找,我们随意的另一个函数的X等于某一个值,然后就能得知他的y值,于是就找到了一个点。
但是这个角度怎么找?
为了方便我们可以这样做:由于直线是可以无限延长的,所以无论如何,只要函数图像不是平行于X轴的直线,那么他就一定可以与X轴相交。
我们把函数的图像和X轴相交的那个点作为顶点,然后以X轴靠近正方向的那一部分作为一个边,然后以这个函数图像在X轴上面的那一部分作为另一个边,我们把这两条边和这个顶点所形成的角称为这个函数图像,或者说是这个直线与X轴的夹角。
如图所示:
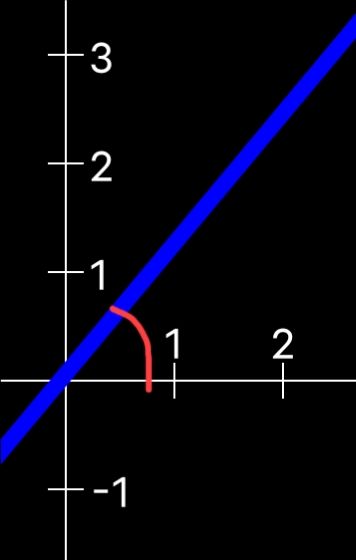
此时我标记为红色的那一部分,就是这个直线与X轴的夹角。
需要注意的是,如果单从这句话来看,直线与X轴的夹角,那么也有可能是左边那个大的角。
但在函数这一部分,我们特指如上文所说的角。
也就是说,并不代表着锐角就一定是我们找的那个角,他也有可能是钝角,比如这样:
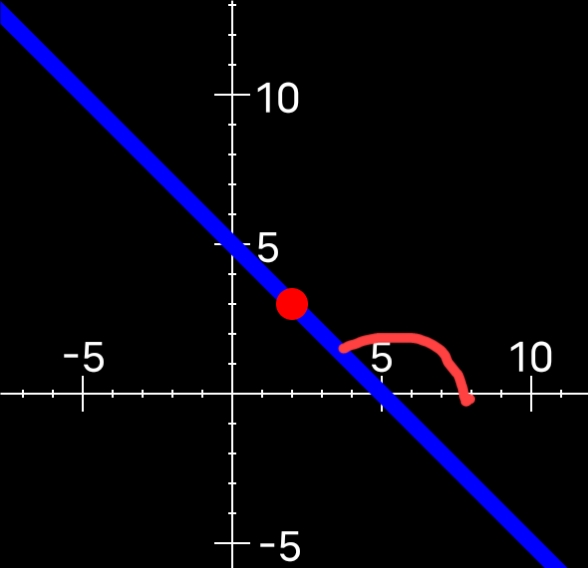
此时我所标记的红色的大角才是我们所要找的那个角。
我们之所以如此苛刻的找到这个角,是为了方便我们更好地描述这个直线。
毕竟如果每个人找的角的标准都不同,那么讨论自然也就没有意义了。所以这件事告诉我们,一定要知道对方在说什么。
好了,那么接下来我们就要尽量把它给标准化。
对了,你们不需要担心,会不会在以后学两条直线的关系时,不知道两直线的夹角是哪个。
我们还没到这里呢,那一部分我们以后再提。事实上,鉴于我可能会忘记,如有可能请你提醒。
好了,我们接下来要把这种角度转化成另一种东西。
事实上思路仍然跟我之前说的差不多。
你需要考虑在X变化时y怎么变化。
比方说,我们仍然考虑Y=X的图像:
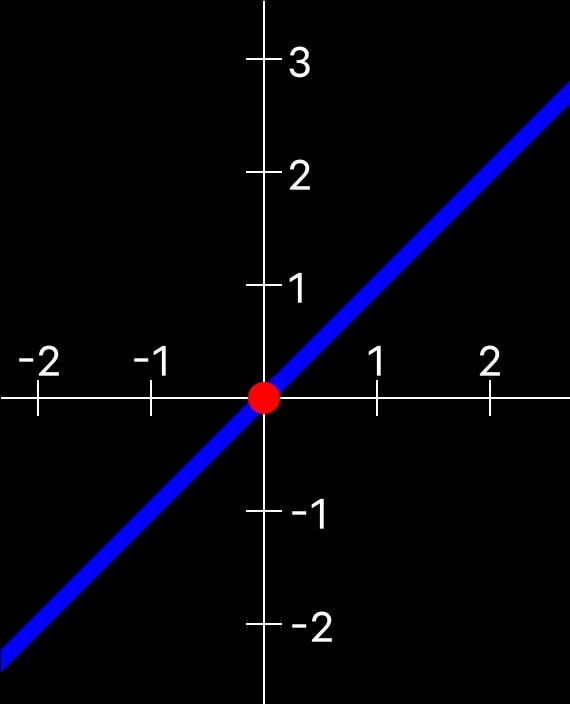
根据我们前面所了解到的,这个图像Y和X以相同的速率增大。
也就是说x增大1y就增大1。
事实上,他们之间有着联系。
图像与X轴的夹角决定了X与Y之间变化的关系。
换句话说,只要这个角度是确定的,我们就一定能够确定X和Y的变化的联系。
在我们的例子中,我们知道夹角为45度时(这个图像的夹角是45度,因为我们知道它是角平分线了),那么他就一定会有X增大1时y也增大1。
换句话来说,这种Y和X之间变化的联系,是由于角度确定的。你也可以这么想,只要确定了X和Y之间的这种变化的关系,那么就意味着知道了他的角度。
所以这两个可以说是可以互相推导出对方。
所以我们知道其中的任何一个就相当于是知道了另外一个。
那么如果我们用角度来描述它的话,会感觉很困难,那么我们不妨就用这种变化的关系来描述这条直线的性质吧!
由于我们说过,y的增加量和X的增加量之间的关系是确定的,所以我们不妨用增加的X的量比上增加的y量,就用它来表示这条直线的有关角度的性质。
比如,我们知道在我们这个例子中,y=x这个图像,当X增加一时y也增加一,所以按照我们刚才的思路,我们就用Y的增加量比上X的增加量,也就是用一比上一。
也就是说,1÷1,那么结果当然还是1。
此时这个最终的结果1,我们给他起了一个新的名字,就叫做斜率。
比较好理解。
因为根据我们刚才的思路,这个斜率的值,就决定了这个图像与X轴的角度,确定了这个角度后,就意味着直观上来看,我们就知道了这条直线倾斜的程度。
所以我们就称呼最终的这个值为斜率。
那么不知道你有没有发现什么东西?
你还记得它的表达式是什么?
y=x。
或者我再提示你一下。
它可以被写为:y=1×x。好吧,我承认,我应该写乘点乘的形式:y=1·x。
我尽力了。
这是否让你想到了什么?
实际上,X前面的数字,恰好就是我们所求出来的斜率。
换句话来说,从这个表达式的角度来考虑,X前面的数字就决定了这条直线的倾斜程度,或者说是这条直线与X轴的夹角。
也就是说,我们可以通过判断X前面的数字,来判断这个直线的倾斜程度,或者角度。随便怎么说,总之,你知道了这条直线的“方向”。
那么剩下的就很简单了。随便带入一个x值,然后找到对应的y值,找到这个点后,你就能够确定它的图像是什么样了。
因为:一个点和一个角度能确定一条直线。
通过这么大篇幅的讲解,我想你应该明白了斜率是一个多么重要的东西。
他一方面可以解答我们X前面的这个数字到底意味着什么,另一方面,它帮助我们确定了这个函数的图像是什么形状的。
再带入一个具体的点就可以画出该图像。
所以斜率还是帮我们大忙的。
不过你还记得我们之前说过的问题吗?
凭什么这么确定这个函数的图像一定是直线?
其实你从我们前面,Y和X增长之间的这种关系应当可以感觉到,他应该就是个直线。
你应该会感觉,它就是应该按照一个直线的趋势进行下去。
你如果能够从这个角度理解的话,其实就已经可以了。
剩下的只是需要一些熟练工而已。
不过就当我拓展一下吧。
说来挺有趣,像这种偏离主要任务的东西,放在其他小说里可能会要被说是水文,不过在学习上,尤其是在数学上,它就摇身一变称之为拓展。
这就是主要矛盾的变化所引发的改变啊。
也许我不应该乱用政治中的词语的。
总之,在下一章,我们将更深刻的认识斜率,并运用斜率来解释刚才的这个问题。














