在我们开始我们的内容前,我想补充一些东西。
其一:缴X和Y这样的未知数,存在几个就称呼其为几元。也就是说存在几个未知数,就叫做几元。
由于我们之前用Y来表示这个含X的式子的一个结果,所以即使这个我们之前所谈论过的一次函数存在X和Y,但是我们仍然认为只有x一个未知数。
所以我们认为他是一元一次函数。
其二:关于次,我之前也提到过,你可以认为次就是这个未知数出现的次数。
我接下来将举例说明一些可能会产生错误的点。
x+1:显然一元一次。
x²+1:显然一元二次。
x²+x+1:当面对这种既有一次又有二次的式子时,我们取最高次,所以他是一元二次。就像游戏里你挑战完最困难的模式后,就能够默认领取前面简单关卡的奖励。
所以我们只在乎那些次数最高的。毕竟他们应付起来也最困难。
那么到现在为止,关于元和次的认识,就到这里了。
我们接下来就引入今天的主题:一元二次函数。
要不要先自己猜一下什么样的是一元二次函数?
或者,你能不能给出一个一元二次函数呢?
就当是我的猜测,会不会给出这样一个呢:y=x²。
我觉得他可以说是最简单的一元二次函数了。
毕竟这是构成一个一元二次函数最基础的东西。
为了方便还是让我们现在给他们起个名字吧!
我们把X右上角的数字称为X的次数。
像上面的x²,可以说这是X的二次方。由于在几何中,通常他会代表着面积,因此又称为平方。
当然,那就不是重点了。
我只想告诉你,这一部分在一元二次函数中被称为二次项。毕竟他是二次的嘛。
而他前面的数字,那就叫二次项系数。
在这个例子中二次项系数为一。
如果是2x²这样的话,那么二次项系数为二。
同样的,如果是X的一次,那么就叫一次项,X的一次前面的数字就叫做一次项系数。
至于数字嘛,比如下面这个具体例子:3x²+2x+1。
最后面的数字一,看起来并未跟X相乘,所以我们称之为常数项。
当然了,既然都叫常数项了,那么也就没有它的系数这一说了。
顺带一提,其实你可以把常数,看成是这个数乘以X的零次方。
因为X的零次方等于一。
当然,我们还是叫它常数项。
说过我们之前说过的那个简单的二次函数。请注意:为了方便,在第二卷中,我们接下来所提到的所有的二次函数都为一元二次函数。
我们刚才说到这个:y=x²。
我们之前的一些经验,到这里可能就不太适用了。
我们并不确定他是否是一条直线。
但是带点仍然是没有问题的。
也许你可以试着,求一求当X等于1,2,3时对应的y置是多少。
那么还有负一,负二,负三。不过他们和1,2,3时的情况一样。因为它们平方后是相等的。
所以,我们现在算一个点,就相当于是把另一个对应的点也求出来了。事实上,只要你做一些简单的思考,你就应该能判断出:这个函数的图像在外周的右边和外周的左边应该是对称的。
很抱歉,在我们没有提到过对称的概念时,就用对称来解释它。不过我相信你们应该明白什么叫对称。
把一张纸对折,如果折过来后,原本折线的两边能够完美的重合,我们就可以说它是对称的。
可以简单的这样想,就是左右差不多,就像翻了个跟头,倒了过来。
就像镜子中的你和现实中的你一样。
那么带点后,至少应该能判断出来,这不太像是直线。你能够感受到图像在快速地往上走。
来看看该图像的几个点吧:
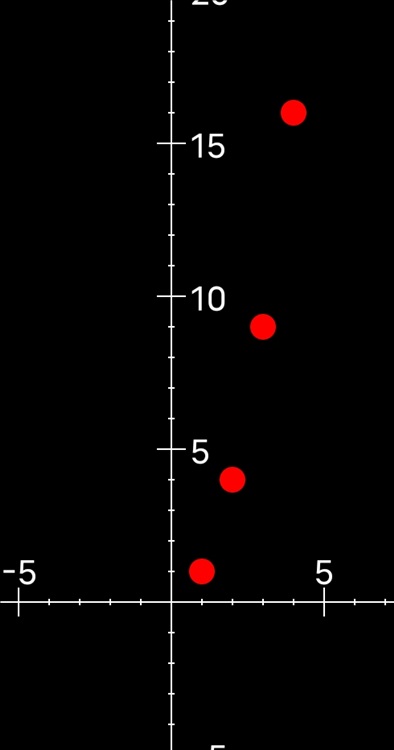
连带着,我将X等于4的点也标记了出来。
现在你能稍微看出一点趋势了吗?
随着X的增大,y在快速的增大。
你能够判断出y会增加的越来越快。
我们并不感到奇怪。
因为我们对X值进行平方,随着X的增大,X平方后的事也一定会越来越大,并且,X从一变成二,X的平方就从一变成四。
当X从二变成三时,X的平方就从四变成九。
你应该可以感觉到y值的增长也是越来越快的。
事实上,我们完全可以用一个更专业的词语来描述我们上面所发现的现象。
实际上我们已经学过这个词了。
那就是斜率。
我们只是发现他现在可以完美的描述,我们现在所遇见的现象。
也许你会说,直线的斜率很好判断出来,那么这样一条曲线又谈何斜率呢?
想解释这个问题,我想要等到以后了,不过按照我们最开始用来描述斜率的那一套比较直观的说法来说,你能够感觉到在X等于一附近时,y的增长量比较小,当然是相对于X等于二附近时。
严格来说,我们最好把“附近”这一个词做一个解释。
不过我们可以先简单的把附近认为是从一开始往左一,再往右一,也就是从零到二这一部分。
你可以看到,他的图像在零到2时y的变化量显然是要小于1到3时y的变化量的。
毕竟,一个是从零到4,一个是从一到九,一个是四,一个是八,那当然是八大。
所以你应该能够体会到,哪怕是这么粗略的看,当X等于2时,这里的“平均斜率”要更大一点。
我这里的平均斜率只是为了更好地描述一下,我们前面的操作,从数值上来讲,它其实就等:当X等于0,1,2,3时,这个图象对应的这四个点,两两作一条直线,这条直线的斜率。
不过最后我还是给一个比较明显的图吧!
还是有点主观印想的好。
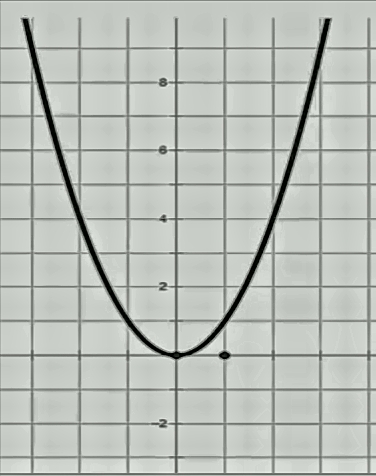
希望这幅图和你自己画的差不多。
总之,我们算是初步了解了二次函数。
接下来,我们要认识各种各样更复杂的二次函数,并试着根据它的表达式来粗略的估计他的大概图像。














