在上一章,我们初步认识了什么是一元二次函数。
并且我们着重的认识了一下,最简单的一个一元二次函数:y=x²。
我建议你把他的图像记住。
这个头像有点像项链,不过更一般而言,人们通常称之为抛物线。
想象一下:如果你往空中扔了一个东西,它的轨迹是不是就相当于把它的图像反过来?所以这个一元二次函数的图像看起来非常像扔一个东西,这个东西的轨迹。
所以我们称之为:抛物线。
当然,数学中也有抛物线这一定义,只不过那可能就会涉及到以后的东西了,我们暂且先不提。
你只需要知道他也叫抛物线就可以了。
顺带一提,你还记得一次函数的图像,是直线吧?
好,关于他的名字相关的东西就到这里结束了。
接下来我们就研究一些更加复杂的二次函数吧!
不过当然,无论多么复杂,只要他还是二次函数,那么就一定是抛物线的形状。
不过在这里我就不向一次函数那样进行证明了,毕竟证明一次函数是直线比较简单一点,相较而言,这个稍微复杂。
并且我想了想,在学这种东西时,好像确实是以主观感受,而非严格的证明来学习的。
好像,在大学之前,不,包括部分大学知识,似乎都是以主观感受为主,而并没有进行严格的“分析”。
所以在此我也不再试图证明二次函数的图像都是抛物线了。毕竟我们还不知道抛物线的定义是什么。
所以以后再说吧!
总之,我接下来将直接给出二次函数的一般式:y=ax²+bx+c.(我忍句号很久了,从现在开始,所有这种字母之类的东西,都以“.”而不是“。”做结尾,因为句号感觉看起来有点乱。事实上,我相信很多人都会在写完这种式子后顺手点点,而非句号。)
不要问为什么不再像一次函数那样用K了,因为他已经没有斜率啦!
不过需要着重强调的一点就是,a不能为零。毕竟,如果a为0的话,那么它实际上就相当于是一个一次函数了。
我们既然在说二次函数,那么一定要满足他有一个二次项。
至于B和C啊,那就可为零可不为零了。
比如我们之前那个简单的例子,那种情况就是B和C都为零的例子。
所以B可以为0,C也可以为零,他们也可以同时为零,他们爱怎么样怎么样,反正只要A不为零就可以。
只要A不为零,那么他就是一个二次函数。
不过,有可能他会给你一种稍微不太普通的式子。
比如:y+x²+x=1.
这看起来有点混乱是吧?
但如果你叫他稍作整理,运用等式的基本性质,我们就可以得到:y=-x²-x+1.
怎么样?这个形式是不是就好多了?
总之,无论他给到你如何复杂的式子,想办法把移动到等式的一边就可以。当然,你还有保证所有的X都在等式的另一边。
就像上面一样。
或者简单来说,想办法只让一个y呆在一边。
这样的话,可以说就是一元二次函数的一般形式了。
不过,这种一般式似乎只是单纯的因为要有二次项,所以才这么写的。
我们看不出来其中的ABC表示什么含义。
正是因为这样,所以二次函数还有另外两种形式。
第一种:顶点式。
这种形式不太常见啊。
但我仍然给出这种形式的式子:y=a(x-h)²+k.
(也不要问这里为什么出现K了,他只是一个字母而已,因为以前的人都这么用哒!)
通过他的名字,以及我刚才的说法,不知道你能不能猜个大概呢?
没错(希望你猜出来了),如果是这种形式的式子的话,我们可以直接读出这个二次函数抛物线上最特殊的那个点:顶点。拿之前的那个例子举例的话,就是(0,0)这个尖尖地方的点。
这个地方我们管它叫顶点。
我还是简单给一下顶点的定义吧:如果像我之前那个例子中它的开口向上,那么顶点就是它的最下面那个点。如果他开口向下,那么顶点就是他最上面那个点。
我们还是拿那个例子吧:y=x².
其实他已经算是一种顶点式了。你能看出来吗?
没关系,让我们稍加改造:
我把X的平方,改为:(x-0)².没问题吧?毕竟X减0后仍然为X。所以平方后一样。
然后,我再在这个整体上加0。
然后再在(x-0)²前面乘上一。
那么我们就会得到以下式子:y=1×(x-0)²+0.
怎么样?改造后虽然看起来比较混乱,但这样的话就和顶点式一模一样了吧?
从这个例子中,你能感受到什么呢?算了,我直接说吧。y=a(x-h)²+k图像的顶点坐标,就是(h,k)。
我想这就是顶点是最有用的地方了
顺带一提,我觉得除了有一些剑走偏锋的题会出跟这个有关的,基本上你遇见的所有题都可以用一般式来解决。
或者交点式。
但是这个交点式虽然稍微的常用一些,但是他有一个很大的弊端:并不是每一个二次函数都可以转化为交点式。
这就得说一下,什么是交点式了。
这是它的形式:a(x-x1)×(x-x2).
根据我们前面的经验,a来源于一般式形式中的a。因为如果你再把他们进行互换的时候,你会发现,这三个式子中的A都是一样的。或许应该这么说,当你在互相转换的时候,这三个A的位置上的数是相同的。
所以我们干脆就统一给他标记为A了。
这算是一个题外话,不过他可能会提前告诉你,在互换时的一些小经验?
不说那些了。
总之,我要告诉你在交点式中x1x2表示什么。
你不妨看看下面这幅图:
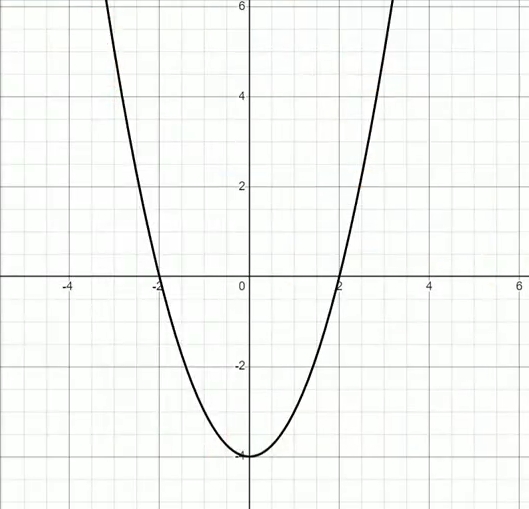
如果这个函数图像可以和X轴有两个交点的话,那么这两个交点的横坐标就是X1和X2了。
至于会不会有x1对应左边x2对应右边嘛,没有。
反正X1和X2这两个值一定是这两个点的横坐标,但他们并没有对应的关系。
就是说,x1可能是左边那个点的横坐标,也可能是右边那个点的横坐标,但无论如何,他一定是这两个点其中一个的横坐标。x2同理。
所以说,你意识到最大的问题了吗?
问题就是:有的图像和X轴没有交点啊!
那这种情况下,你这个交点式还写不写的出来呢?当然就写不出来了。
所以,如果你知道它的图像的话,才能够很轻松的写出它的交点式。
而且如果这个图像和X轴没有交点的话,你甚至写不出来。
所以一般而言,这个也不是很常用,不过我希望你能知道。
事实上,我认为绝大部分的题,你用一般式就可以解决了。
除非有特别明显的那种,直接告诉你顶点坐标,或者告诉你和X轴交点坐标,这种非常方便你写另外两种形式的信息,你在考虑这另外两种方法吧。
那么接下来,我们会将主要精力都放在一般式上面,并以此为基础继续研究一元二次函数的性质。














