我们再次来回顾一下这个最简单也是最基本的二次函数吧,y=x².我们将以此为基础, 继续深入探究二次函数。
你还记得我之前曾说过的一件事情吗?有关于对称的事。对于这个函数(y=x²)来说,这个函数在x轴的正半轴和x轴的负半轴的图
像是差不多的。或者说,它们只是颠倒了一下方向。这一点你可以轻易的看出来。比如1和-1平方后都为同一个数1。其他的也类
似。x从零开始,向左向右只要移动的距离相等,那么他们平方后的结果就相等。
也许我们可以用这个式子来表示。(0+a)²和(0-a)²。我得做个解释。a在这里表示从0开始,在x轴上移动的距离。那么第一个加
法的式子就表示向右移动a后的x值,再进行平方得到的结果。同理,
第二个加法的式子就表示向左移动a后的x值,再进行平方得到的结果。显然,他们最后的结果都是a的平方。无论是正a还是负a平
方后都一样。至于0,它没有影响,对吧?
无论如何,我们算是简单的证明了从0开始,向左向右移动同样距离的x所对应的y值都相等。换句话说,也就是我们之前所说的“对称”。
接下来,我们想一想这个式子,y=ax².刚才上面所说的那个例子,可以看成是a取一时的特殊情况。当然了,上面所说的所有,都是
二次函数的一般式y=ax²+bx+c中的b和c都取O的特殊情况。
不过还是让我们把目光聚焦于a上。让我们来考虑一下,a究竟怎么影响二次函数?也可以这样说,当a发生变化时,这个二次函数的图像会发生怎样的变化?
想要知道图像发生了什么变化,首先我们总得知道它的图像吧?我们曾经找了一些y=x²图像上的一些点,还有印象吗?如果有的话那很好,没有的话也没有关系。你很容易想到,随着x值从小变大,那么它们所对应的y值会变大的越来越快。
当然,这里的x是从0开始变大的。如果x从0开始变小呢?我们前面已经提到过对称,他应该和变大是一个相同的趋势。当然,这种所谓的趋势都是从0开始的。不能说因为对称所以x在0左侧的区域也是从左往右逐渐变大。也许应该这么说,X值从0开始,往左右两侧都要大。总而言之,我们可以轻易的想象出他的图像。不过还是让我们来看一看吧。
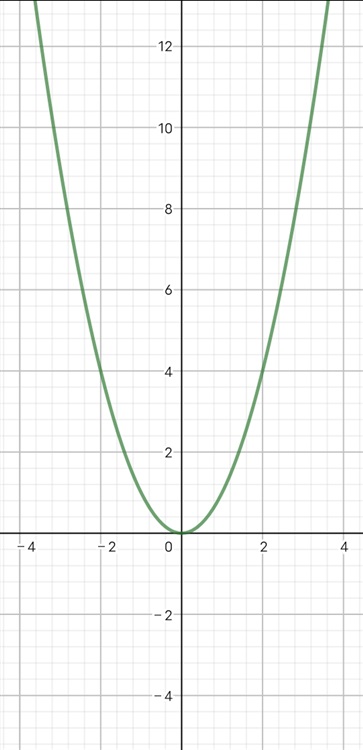
这就是b和c都取0,同时a取1时的图像。a,b和c是指二次函数一般式的对应系数。
接下来我们仍然让b和c为0,只改变a来看一看它究竟是怎么影响这个二次函数的。
我们先把a变成2吧。也就是说此时的二次函数应该是y=2x²其实结果比较显而易见,无非就是在原来的基础上乘2。当然,是每一个对应的x都乘2。所以这个新函数的每一个y就相当于原来的y乘2。
那对应到图像上,我们可不可以这样说,就是它相当于把原来的函数图像向上“拉伸”了。你可以这样想象一下,把原来的函数图像当成一根垂着的绳子,你一只手抓住原来那个函数的顶点,另一只手抓住绳子的上面,然后用力往上一拉。
说了这么多,你应该大概知道他的头像是怎样了的吧?
就像刚才一样,我们再来看一看,它的图像。
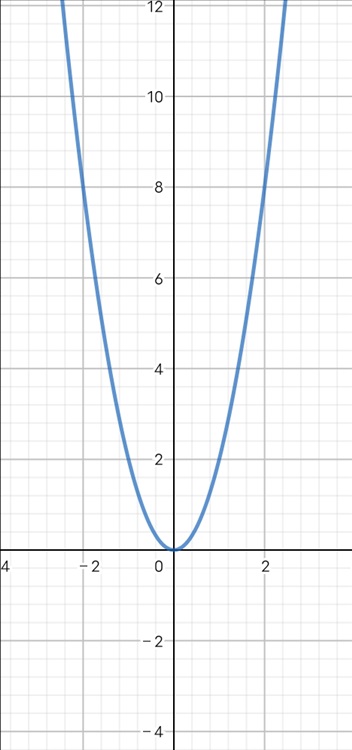
跟上面比起来,真的很像是把它往上拉了一下,对不对?
接下来,让我们把它们放在同一个坐标系里,这样你能够更加直观的看到他们的变化。
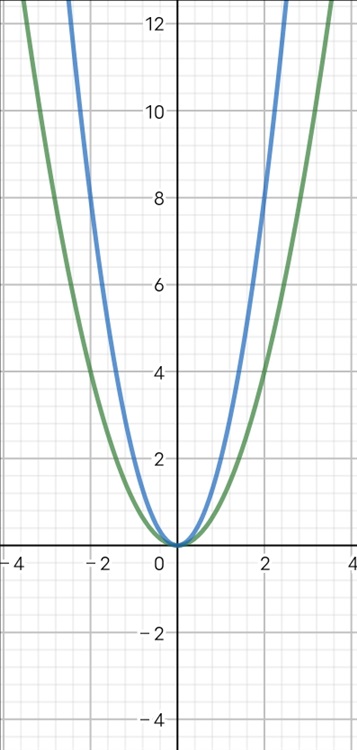
对比着来看,就比较明显了吧?
不知道你有没有一种感觉,当我看到这幅图的时候,我的想法是,变成二倍之后就这?看着好像靠的也挺近啊。
不过你可以仔细的看一看,比如你可以想象有一把锋利的剑从正上方竖直的往下穿过,这把剑划过的痕迹,将会与这两条抛物线形成两个交点。
这两个交点的y值一定会是一个二倍的关系。
你可以去试一试,或者你也觉得这是一个显而易见的结论,那我们就继续了。
这件事告诉我们,不要太过相信直观的感受。
你说什么?你一眼就看出来上下是二倍的关系?或者说你感觉就像是二倍的关系?
好吧,那你就当我刚才什么都没说吧。
不过不管怎样,希望刚才的图能为你带来一些直观上的印象。
我们现在要考虑一下,a究竟怎么改变这个二次函数。
经过刚才观察a从一到二的变化,我们不难发现就是现在图像的所有y值都变成了原来的二倍。
事实上有一个更好的说法。
y值变成了原来的a倍。
只不过在刚刚我们那个特殊的例子中,由于a取2,因此就是二倍。
这一点从表达式上很容易观察到,y=ax²,我们可不可以把它理解成,y等于a倍的,1倍的x².我这里把一倍单独说了一下,是为了强调,我们所说的a倍是什么的a倍。
不过刚才仅仅是从数值上说明a对这个二次函数造成了什么变化,那如果我们从整体的图像来看呢?
把所有的图像都往上移了一点?
不对呀,零那个位置没有变化呀。
再者说了,不同位置,他网上变化的量不同啊。
不知道你能不能感受到,我们似乎很难从纵向去描述它的变化。
当然横向似乎也比较难。正如我们最开始说他像绳子被拉伸那样的描述,你也可以说图像像是从左右压扁了。
似乎都有点困难。
不过我想也不会有人非要你给出一个纵向或横向变化的量与a的关系。
事实上纵向比较好给。我们考虑任意一个X值,两个图像y值相差的量,应该等于它们各自的表达式之差。
比如如果当a等于2时,它们的差应该是:2x²-x².我之所以采用减法而没有给出结果,是为了方便你把二替换成a,这样你就知道任意两个二次函数任意x值的差值了,也就是对应的y值的差值。
横向的如有机会我们再说。
事实上,我们有一种更好的方法来描述a的作用。
我们可以认为决定了这个抛物线上端的开口大小。
也许你有疑问,作为一个没有尽头的图像,他哪里来的开口呢?也许他应该只是把这个平面直角坐标系分成了两个部分,毕竟这是一条没有尽头的曲线。
不过如果你假设在某一个地方忽略上面的图像,就像我们刚才展示的图片一样,不再去想图片上方图像应该是怎样的,而是只注重图片给出的这部分图像,假设他有一个开口的话,那么a就决定了这个开口的大小。
也许还有一些更形象的说法,比如,a决定了他的胖瘦。
总之,这种描述是为了让你更好地向其他人表述的作用,在此之前,你首先应该注重的是明白它的作用,而不是会表述它的作用。
不过a只决定的是一个东西吗?我们并没有考虑负数的情况。
接下来我们将把负数的情况一并考虑在内,看看这个a到底决定了什么。














