「折射定律,入射角与正弦角的正弦值之比为n,这个值取决于两种介质的性质:
皮埃尔·费马解出n为u1/u2,即光在第一种介质中的传播速度除以第二种介传,那么借此可以将公式移项改写成:
设想一下这个问题中从a点下滑到b点的并非一个受重力作用加速的质量块,而是从a点移动到b点的一束光射入密度递减的不同介质层时,速度越来越快;
E=T+V:
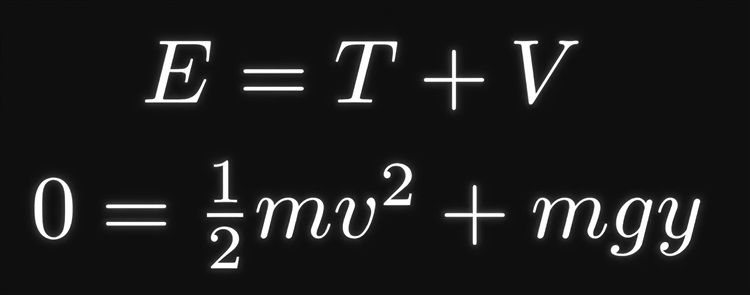
在下落一段距离y后的任意时刻,粒子速度的平方与y成正比:
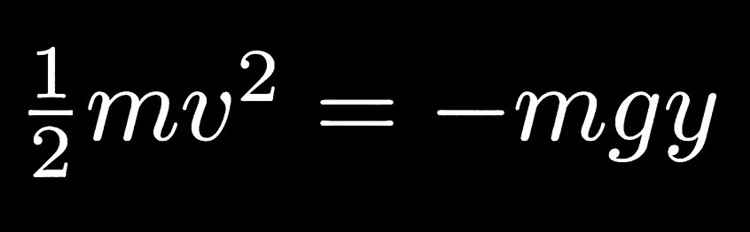
因此速度与根号y成正比:
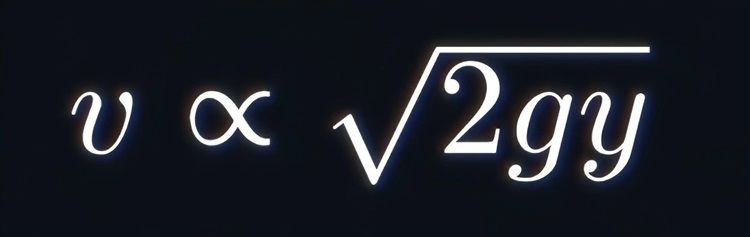
这一情况可以类比为光在特定介质中的非匀速传播,而是光速与顶部的距离成正比;
这时将每层的光速表达式代入折射定律,就会发现第一个角的正弦值除以第一层y的平方根,等于第二个角的正弦除以第二层y的平方根;
等式可以继续延长到Θ3的正弦处以y3的平方根:
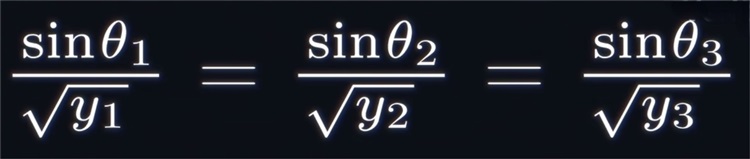
换言者这个这个比值等于常数k:
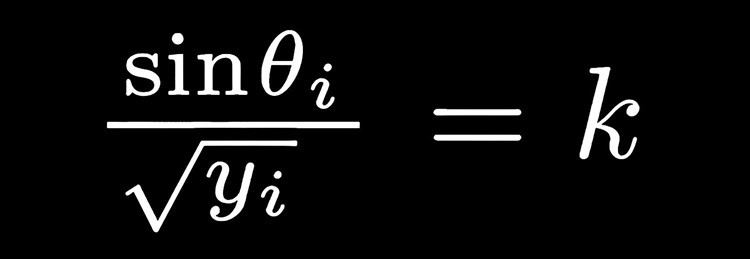
这其实也是一个摆线方程:

从a移动到b点的最快路径就是沿着摆线的一段弧,不是圆,而是摆线。
这段ab摆线弧有趣的地方在于,无论你从哪个点释放同一物体,最终都会在同一时间到达终点;
故也被称作“等时降线”(Tauto chrone curve),源自希腊语,就是所谓的同一时间。
发现这个公式的伯努利也相当于“解决了一个光学问题,一个力学问题。“两个截然不同领域的数学问题,本质相同。”」
古特曼先生拧开他的茶叶杯,很显然他很热爱东方的茶叶。茶水分离的过滤层泡满满了普洱。
「通过这个问题,伯努利的学生敏锐地注意到了一些更深层次的真理。
他的学生皮埃尔在研究光和粒子的行为时发现二者极为相似,他在思考“为什么自然要在乎最小时间化?”
如果自然界存在一个更基础的量呢?
这个量制约着光,也制约着粒子?
“作用量”油然而生,全新的术语被其引入。
移动越远,作用量越大;
速度越快,作用量越大;
粒子质量越大,作用量越大。
分段路径的总做用量可以书写为各段质量*速度*距离总和:
假设没有摩擦、损耗、介质的变量,光线射入一段液体后为何一定是等比折射角的根本原因在于,可折射的所有角度里,折射角的质量*速度*距离总和为最小值;
这个皮埃尔因此提出,“作用量才是自然的真正开销,自然之母设法使之尽可能小。”
欧拉将这个公式做了优化,他将积分代替了求和:
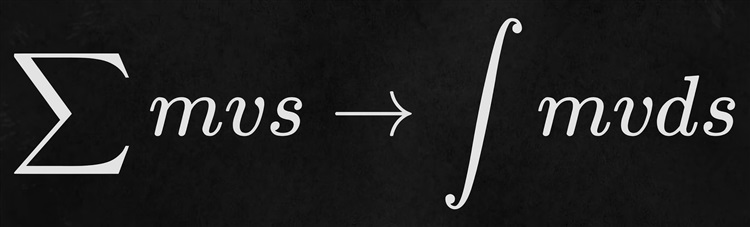
以此来计算粒子绕中心质量的运动轨迹;
他意识到a点到b点的最小作用量原理必须在总能量守恒时才能成立,且对所有路径能量都得相等。
欧拉提升了最小作用量定理的数学严谨性,但距离一般性证明还有一段不小的距离。
后世的拉格朗日横空出世,他给出了最小作用量的一般性证明;
假设a点与b点间有无数条可通过线段。拉格朗日选择从函数上寻找极值,对函数求导并令导函数=0:
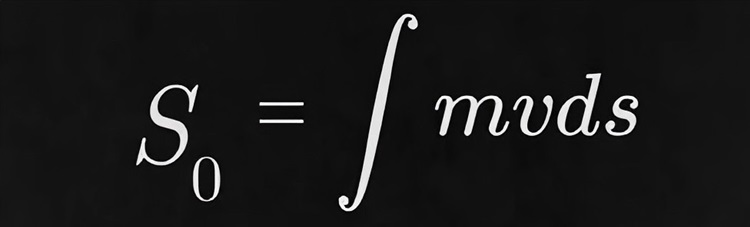
↓
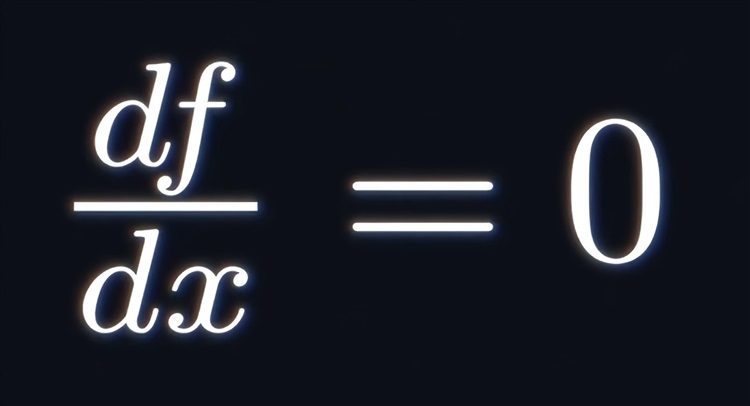
在函数图上的该位置斜率水平必然会取得极值,极值曲线上的变化应正比于η的平方或更高次项:
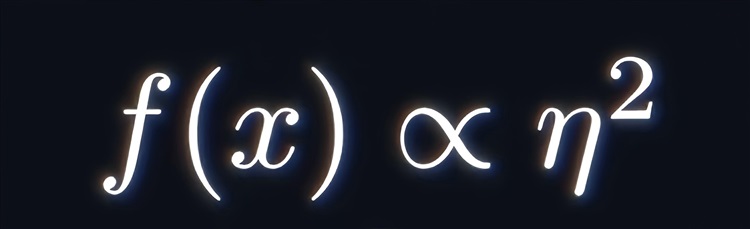
↓

这便是当时的最小作用量原理一般性证明。现在我们进行现代化转化。首先欧拉引入的积分证明以及系统内的能量守恒,再利用莱布尼兹法则的导数计算;
那么哈密顿原理就是最小作用量原理的现代形式,也是几乎所有物理书上的书写形式:
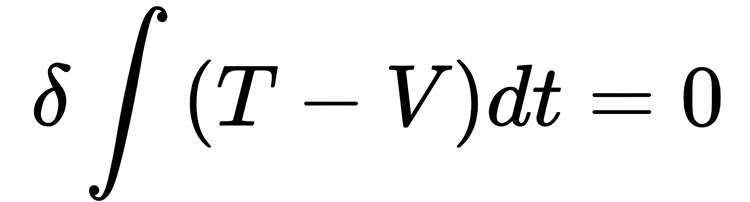
可以看出哈密顿是站在拉格朗日基础上的最小作用量原理现代形式...」
………














